RNN과 LSTM 톺아보기

in Data Science on Deep Learning


💡 RNN과 LSTM 대해서 알아보자 (자세한 수학적 내용보다는 개략적인 이해를 위한 내용만 담았습니다)

1. 복습을 해보자…

인공신공망의 기억을 떠올려보자

Perceptron(퍼셉트론)

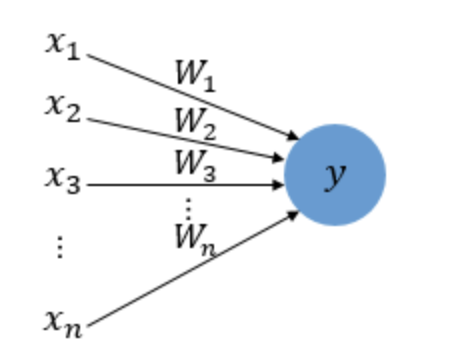
rnn_lstm_1.png

MLP (Multi-layer Perceptron : 다층퍼셉트론) = DNN

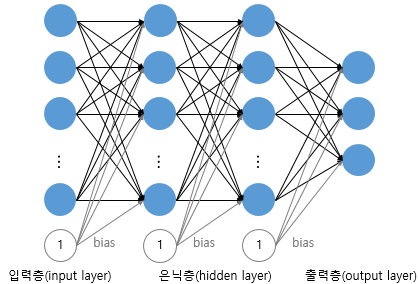
rnn_lstm_2.png

간단히 이렇게 나타냄,,

rnn_lstm_3.png

2. 순환신경망(RNN)

일반적인 DNN을 보면, 은닉층을 지난 값은 모두 출력층으로만 향한다.

rnn_lstm_4.png

하지만 이렇게 은닉층을 통해 나온 결과값을 출력층에도 보내면서 다음시점의 은닉층 노드에도 보내는놈을 RNN(Recurrent Neural Network. 순환신경망) 이라고한다.

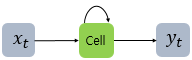
rnn_lstm_5.png

간단하게 이렇게도 나타낸다. (은닉층에서 나온 output을 은닉층에서 또 활용하는 재귀적인 모양.. =재귀신경망이라고도함)

이는 $x_t$ 를 계산하기 위해서는 $x_{t-1}$에 대한 계산도 도움이 되지않을까? 라는 철학에서 시작됨

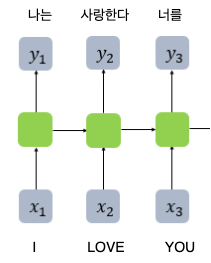
rnn_lstm_6.png

가령 위와같은 영어→한국어 번역모델이있다고할때, love 를 사랑한다 라고 해석할 때, I 에대한 해석(=I에대한 은닉층의 output)이 충분히 도움이 될거라고 생각하고, 해당 은닉층의 값을 같이 활용하는것이다.

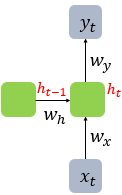
rnn_lstm_7

시점 t에서는 메모리에 따로 저장해놨던 $h_{t-1}$과 $w_h$ 를 모두활용하여 $h_t$를 구하게된다

은닉층 : $h_t = tanh(W_xx_t + W_hh_{t-1}+b)$

출력층 : $y_t = f(W_yh_t + b)$

1) pytorch로 RNN 구현해보기

import torch
import torch.nn as nn

input_size = 5 # 입력의 크기
hidden_size = 8 # 은닉 상태의 크기

# (batch_size, time_steps, input_size)
inputs = torch.Tensor(1, 10, 5)

cell = nn.RNN(input_size, hidden_size, batch_first=True)

outputs, _status = cell(inputs)

3줄이면 구현됩니다. (실화입니다..)

2) DRNN (Deep Recurrent Neural Network)

rnn_lstm_8.png

별거없고 은닉층이 이런식으로 깊어지면 DRNN이라고한다

3) BiRNN (Bidirectional Recurrent Neural Network)

아마 위의 철학을 들었을때, 이렇게도 생각했을수있다.

그럼 과거시점의 데이터뿐아니라 미래시점의 데이터까지도 중요한거아닐까?

Exercise is very effective at [          ] belly fat.

1) reducing
2) increasing
3) multiplying

정확한지적이다.

가령 위와같은 빈칸채우기문제에서 ‘운동은 복부 지방을 [] 효과적이다’ 에서 reducing이라는 단어가 정답이라는걸 예측하기 위해서는 at 뿐만아니라 belly fat 이라는 단어도 큰 힌트가 될것이다

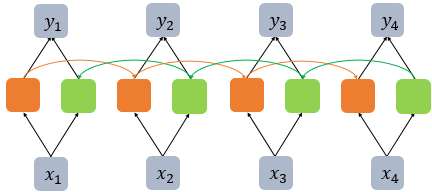
rnn_lstm_9

그래서 이렇게 앞의 은닉층과 뒤의 은닉층 모두의 정보를 전달받아 출력값을 계산하는 모델을 BiRNN(양방향 순환신경망) 이라고한다.

3. 장단기 메모리(Long Short-Term Memory, LSTM)

1) 바닐라 RNN 의 한계

rnn_lstm_10

예전에 Vanishing Grandient(기울기소실)에 대해 배운적이 있다. 은닉층이 깊어질수록 전달되는 오차가 줄어들어 학습이 되지 않는 현상이다.

비슷하게 바닐라 RNN에서도, 위 그림과 같이 time step(시점)이 길어질수록 (ex. 번역모델이라면, 문장이 길어질수록) 앞의 정보가 점점 뒤로 전달되지 못하고 소실된다. 뒤로갈수록 $x_1$의 정보량은 손실되고 영향력은 미미해진다.

이를 장기의존성문제라고한다.

2) LSTM (Long Short-Term Memory)

rnn_lstm_11

LSTM은 은닉층에 입력 게이트, 망각 게이트, 출력 게이트를 추가하여 불필요한 기억을 지우고, 기억해야할 것들을 정한다. 한마디로 정보의 중요도를 조절하는 수도꼭지를 추가하는거나 마찬가지..

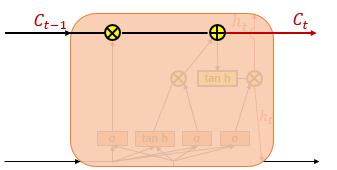
rnn_lstm_12

이 수도꼭지들을 통해서 중요한 정보들은 바뀌지않고 그대록 흐르게되어, 장기 의존성 문제를 해결하게된다.

그렇다면 각 게이트들이 정확히 어떤짓을해서 이게 가능할까?

3) 입력게이트

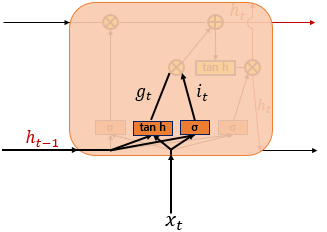
rnn_lstm_13

현재의 정보를 기억하기 위한 게이트

tanh, 시그모이드 모두 activation function의 일종. (값을 normalize 해줌)

$x_t$와 $h_{t-1}$을 여기에 넣어서 현재정보를 얼마나 기억할지를 조절하게된다.

4) 삭제게이트

rnn_lstm_14

기억을 삭제하기위한 게이트.

$x_t$와 $h_{t-1}$을 시그모이드에 넣어서 정보를 얼마나 삭제시킬지 구하게됨

0에 가까울수록 많이 지우게되고 1에 가까울수록 적게지우게됨

5) 셀 상태

rnn_lstm_15

$C_t$가 시점 t의 셀 상태인데 이를 long-term state(장기 상태)라고도 함.

$C_{t}=f_{t}∘C_{t-1}+i_{t}∘g_{t}$

  • $f_{t}∘C_{t-1}$ : 삭제게이트의 결과만큼 이전셀의 상태값을 삭제 (=기억을 지움)
  • $i_{t}∘g_{t}$ : 입력게이트를 지난 두개의 값을 곱함 (=기억할걸 선택함)

이렇게 두 값을 더하여 셀 상태를 구하고, 이 값은 다음 t+1 시점의 LSTM 셀로 넘겨짐

6) 출력게이트

rnn_lstm_16

$o_{t}=σ(W_{xo}x_{t}+W_{ho}h_{t-1}+b_{o})$ $h_{t}=o_{t}∘tanh(C_{t})$

출력 게이트는 $x_t$ 이전 시점 $h_{t-1}$가 시그모이드 함수를 지난 값. = 이녀석이 $h_t$ 를 조절하게됨.

$h_t$는 short-term state(단기상태)로, 장기상태 $C_t$가 tanh를 지난 -1 ~ +1 사이의 값을 출력게이트로 조절한값이다. 시점t의 최종 output을 계산하고 또한 다음 t+1 시점의 LSTM 셀로 넘겨짐.

7) 파이토치의 LSTM

기존3줄코드에서 RNN 모델 선언부분을 LSTM 으로 바꿔주기만하면된다.

nn.LSTM(input_dim, hidden_size, batch_fisrt=True)



© 2020. by berrrrr

Powered by berrrrr