가능도(likelihood)와 최대가능도추정(MLE)

확통의 기억을 되살려보자…

1. 확률 (Probability)

주어진 확률분포가 있을때 관측값(or 관측구간)이 해당 확률분포 안에서 얼마의 확률로 존재하는지를 나타내는 값.

확률 = P(관측값X | 확률분포D)

ex. 주사위를 던져서 1이 나올 확률 = 1/6

ex. 동전 10번을 던져서 앞면이 2번 나올 확률 = 0.044

2. 연속사건의 확률

2.1 특정 사건의 확률은 모두 0

특정 사건의 확률은 모두 0임.

뭔말이냐?? ex. 1과 6 사이의 유리수에서 정확히 숫자5를 뽑을 확률은? 1/무한대=0

연속된 숫자는 무한하므로 특정 숫자가 나올 확률은 의미가 없다

( = 연속된 사건에서 특정 사건이 발생할 확률은 의미가 없다)

2.2 특정 구간에 속할 확률 = 확률밀도함수(PDF)

그럼 연속된 사건 안에서 확률을 구할 방법이 전혀없는가? 그건 아님.

특정사건의 확률 대신 특정 구간에 속할 확률을 구하면됨.!

ex. 정확히 5를 뽑을 확률은 알수없지만, 대충 1과 6사이 숫자에서 4와 5사이 숫자를 뽑을 확률은 20%임을 알수있다. (5칸중에 1칸이니깐)

확률밀도함수(Probability Density Function, PDF) : 특정 구간에 속할 확률을 계산하기 위해 확률을 밀도로 나타낸 함수.

그래프에서 특정 구간에 속한 넓이=특정 구간에 속할 확률

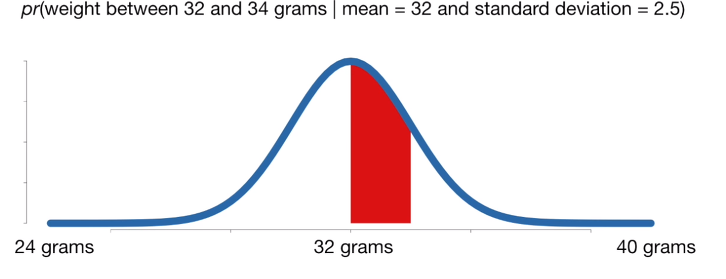
ex. 귀여운 쥐들의 몸무게가 평균 32 표준편차 2.5의 정규분포를 따른다. 이때 쥐의 무게가 32-34 사이로 관측될 확률은 빨간 영역과 같다

3. 가능도(Likelihood)

연속사건에서 특정 사건이 일어날 확률은 위에서 설명했듯이 0…

근데 확률밀도함수보면 특정 사건이 일어날 확률이 언제가 높을지는 대충 보이잖음.. (y값이 높을수록 그 사건이 일어나기 쉬움)

이렇게 주어진 관측값이 해당 확률분포에서 나왔을 확률(=PDF의 y값)을 가능도(likelihood)라고함.

ex. 내가 쥐를 하나 골라서 무게를 쟀더니 34g이 나옴. 이때 관측결과가 (평균=32,표준편차=2.5)인 정규분포에서 나왔을 확률은 0.12 가능도임. (평균=34,표준편차=2.5)인 정규분포에서 왔을 가능도는 0.17로 더 높음.

4. 최대가능도추정(Maximum Likelihood)

관측값에 대한 총 가능도(모든 가능도의 곱)이 최대가 되게 하는 분포를 찾는것.

쥐 무게를 재서 이런 관측값들을 얻었다고하자. 이 데이터들은 어떤 정규분포에서 왓을까?

각 샘플별 가능도의 곱을 구해서 회색공으로 표시해보니, 중간에 위치한 정규분포에서 나왔을 확률이 젤 높다. 이렇게 총 가능도가 최대가 되게 하는 분포를 찾는게 최대 가능도 추정(MLE)이다.

http://rstudio-pubs-static.s3.amazonaws.com/204928_c2d6c62565b74a4987e935f756badfba.html

https://bookdown.org/mathemedicine/Stat_book/probability-vs-likelihood.html

https://jjangjjong.tistory.com/41 이게 젤쉽게정리된듯