linear discriminant functions for classification (분류를 위한 선형 판별식)

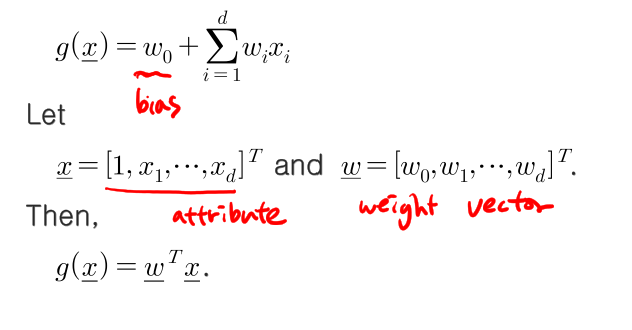
g(x) = w0 + d∑wixi
W0=bias wi = i번째 weight vector(가중치 벡터) xi = i번쩨 attribute (특성벡터) 벡터 x = [1,x1, ...xd]^T , 벡터 w = [w0, w1, ... wd]^T 라 하면
g(x) = w^Tx 로 표현할 수 있다.

binary classification

c1, c2 2개 클래스로 분류하기.
만약 w^Tx > 0 이면 c1 클래스이고
그 외면 c2 클래스이다.

xi가 c1 에 속한다면 w^Txi > 0 (양수. positive)
xi가 c2 에 속한다면 w^Txi < 0 (음수. negative)
근데 c2일때 xi 라벨에 -를 붙여서 -xi로 만든다고한다면 w^T(-xi) > 0 (positive).
따라서 올바르게 classify를 한다면 w^Txi > 0 (inner product는 항상 양수..)

Perceptron criterion function

이때 x는 X(w)에 속하고, X(w)는 잘못분류되는 모든 sample set을 의미.
misclassify이면 innerproduct 값이 음수. -> Jp(w)는 양수
정상적으로 classify면 innerproduct값이 양수. -> jp(w)는 음수
따라서 Jp(w) (Perceptron criterion function)을 최소화하는 방향으로 학습을 진행해야함.

gradient descent algorithm

weight는

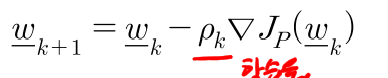
Jp의 변화량은 Jp의 기울기.. 따라서 gradient는 convex한 형태를 따라 점점 낮은값으로 갈수밖에없음..

(1) Batch mode

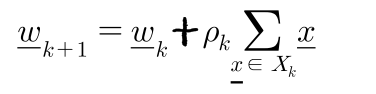
모든 sample을 써서 한 gradient를 계산한다. (linear model. convex model. 선형모델일경우에는 유리하다.)

(2) on-line mode (incredental mode)

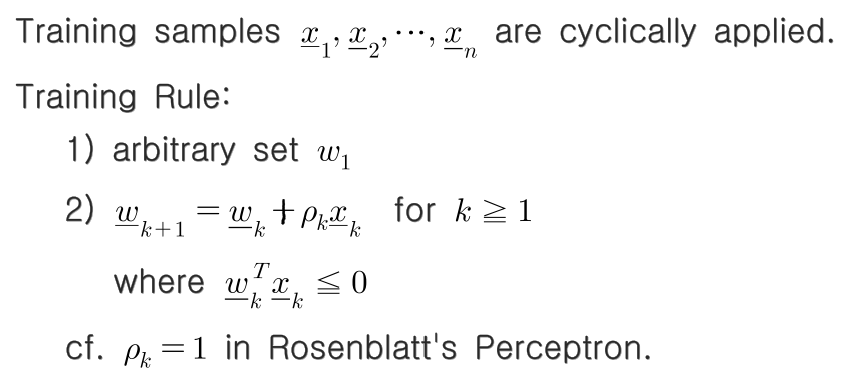
한 sample을 써서 gradient를 계산한다.(stochastic gradient)
local minimum problem때문에 보통 on-line mode의 정확도가 더 높다. (non-linear model. non-convex model 일경우 더 유리하다)