Decision Tree representation

• Decision Tree learning은 approximating(근사치)를 구하는 방법이다.
• 각 value의 target function은 decision tree로 표현된다.
• Decision Tree는 if-then rule로 쉽게 표현할수있다.
• Decision Tree에서 각 internal node는 attribute(속성)을 테스트하고 각 branch는 attribute value(속성값)에 응답하고 각 leaf node는 classification(분류, 결과)를 결정한다.
• 일반적으로 decision tree는 instance의 attribute value(속성값)에 대한 contraints(제약조건)을 분리하여 나타낸다.

ex) xor 에 대한 decision tree

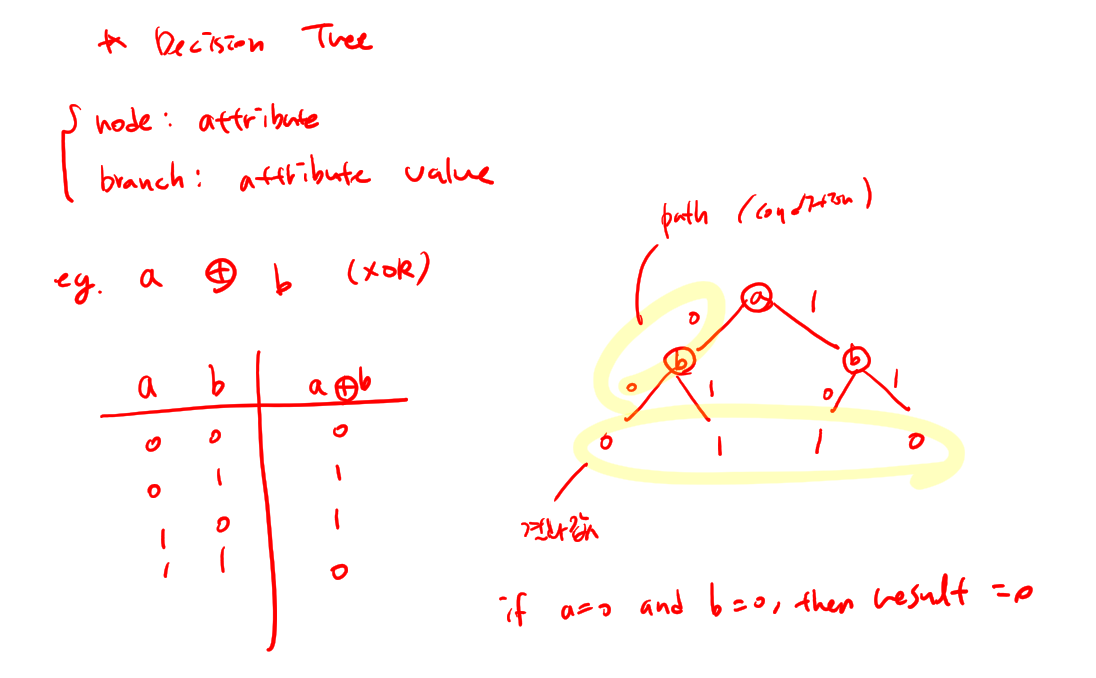
Target function

우리가 X input을 넣었을때 Y output을 넣는 방정식을 얻고자 한다면 f:X->Y 가 target function이 된다.

appropriate problems of DTL

DTL을 사용하기 적절한 문제

• 속성-값 쌍으로 묘사될수있는 문제
• target function이 discrete value인 문제
• disjunctive hypothesis가 요구되는 문제
• training data에 noise가 있을수 있는 문제 (entropy를 사용) e.g > 의료(병) 진단, credit risk 분석, 스펨메일 필터링 등..

learning algorithms of DTL

1. CART
2. ID3 (entropy를 사용)
3. C4.5 (ID3 알고리즘을 개선)

ID3 algorithm

Step.1 가장 classification 잘되는걸로 root node 결정. Step.2 (1) A <- 다음 노드를 결정하기에 가장 좋은 속성을 A로 한다. (2) A를 node의 decision attribute로 놓는다 (3) A의 각 value에 새 하위 노드를 만든다. (4) leaf node에 학습 샘플을 배치 (5) 만약 학슴샘플이 완벽히 분류되면 멈추고 아니라면 새 leaf node를 만든다.

Entropy

S 가 training example의 샘플이라고할때
p+ 는 S가 positive sample일 확률
p - 는 S가 negative sample일 확률이라고하자.
이때 S의 entropy는
Entropy(S) = -p+log2p+ - p-log2p- 이다.
Entropy는 c개로 분류하기위해 (위의 경우에는, +인지 -인지구분하기위해) 얼마나 많은 bit수가 필요한지를 나타낸다.
target attribute가 c개의 다른 value를 가진다면 entropy(S)는 c개의 -pilog2pi를 summation한 값이다.

Information gain

reduction of entropy by selecting a certain attribute(node).
속성을 선택하여 uncertain한 요소를 제거하여 entropy를 점점 감소시키는것.
A속성일때의 Information gain값은 전체 Entropy에서 A에 해당하는 value값을 가지는 경우의수/전체경우의수 * Entropy(A에해당하는 value를 가지는경우) 를 모두 빼준값이된다.
이 Information gain값이 높은 속성일수록 가장 Entropy를 떨어뜨리는 속성이 된다.

Hypothesis space search by ID3

• hypothesis space H가 complete 하다는건 target function이 확실하게 H 에 속해있다는것을 의미한다.
• ID3는 하나의 가설을 생성한다.
• backtracking 없이 ID3는 decision tree에 응답해 locally optimal solution (지역적 최적화 해답)을 생성해낸다.
• information gain을 이용한 통계적 기반의 search이기때문에 noisy data에 대해 강력하다.

inductive bias in ID3

• 짧은 tree일수록 정확도가 좋다
• 가장 큰 information gain을 가지는 attribute를 가장 root에 가깝게 배치해야 좋다.
• inductive bias가 없으면 모든 possible한 가능성을 뒤져야하기때문에 inductive bias가 필요하다.

overfitting of ID3

decition tree의 분기 수가 증가하면 training data는 잘 설명하지만 이외 data는 잘 설명하지못하는, 즉 generalize가 되지 않는 overfitting(과적합) 현상이 일어난다.

methods to avoid overfitting

overfitting(과적합)을 막는 방법

• data가 통계적으로 유의미하지않다면 tree를 늘리지 않는다
• full tree를 만든 다음 적당한 시점에서 pruning(가지치기)를 해준다
• best tree를 선택한다
  1. training data의 성능을 측정
  2. separate validation set의 성능을 측정
  3. tree의 크기와 misclassification을 최소화
• reduced error pruning 가지치기 오류를 줄이려면
  1. data를 training set과 validation set으로 나눈다
  2. pruning이 더 손해보기 전까지 아래 과정을 반복한다. 1) 각 node를 가지치기한 validation set의 impact를 측정 2) 탐욕적으로 가장 validation set의 정확도를 향상시키는 것을 확인하고 가지치기함.
• rule post-pruning (C4.5) : ID3보다 더 개선된 방법. 더 effective하다. 그 rule이 valdation set에 맞는지를 판단.
  1. training data가 최대한 잘 fit해질때까지 단계를 늘린다
  2. tree를 if-then 방식으로 치환해본다
  3. 정확도를 향상시키도록 rule을 가지치기한다.
  4. 정확도로 각 가지키기된 rule을 정렬한다.

improving ID3

• continuous value 속성 : 연속적인 속성을 특정 interval을 가지는 discrete set으로 나눠서 동적으로 정의된 새로운 discrete-value 속성으로 만들어야함. 여러 방법이 있겠지만 그중 하나는 가장 큰 information gain을 가지는 threshhold를 설정하는것이다.
• 여러 value를 가지는 속성 : 많은 가능한 value가 trainig example을 다른 더 큰 training exmaple 세트보다 information gain을 더 크게 가질수있도록 작게 쪼갤수있도록 지정한다.
• 여러 방법 중 하나는 information gain 대신에 gain ratio를 사용하는 방법이 있다. gain ratio는 information gain을 split info로 나눈값이다.

참고 https://jihoonlee.tistory.com/16?category=725291 https://blog.naver.com/tkdgbtkdgb/221650800350